3.1.1Открытые множества и окрестности¶
Теперь мы введём следующее, очень важное для дальнейшего, определение.
Proof
Если бы множество было бы открыто, то для любого можно было найти такую -окрестность , что , но множество состоит всего из одной точки, а любая -окрестность точки состоит более чем из одной точки. Поэтому включение невозможно, поэтому множество не открыто.
Proof
Пусть — интервал конечной длины, тогда на него можно посмотреть как на окрестность точки (= середина отрезка) с радиусом , итак
Рассмотрим произвольную точку , отличную от точки , т.е. и рассмотрим её окрестность , где . Покажем, что , это и докажет требуемое.
Возьмём произвольную точку , тогда , а в силу выбора δ, мы также получаем, что
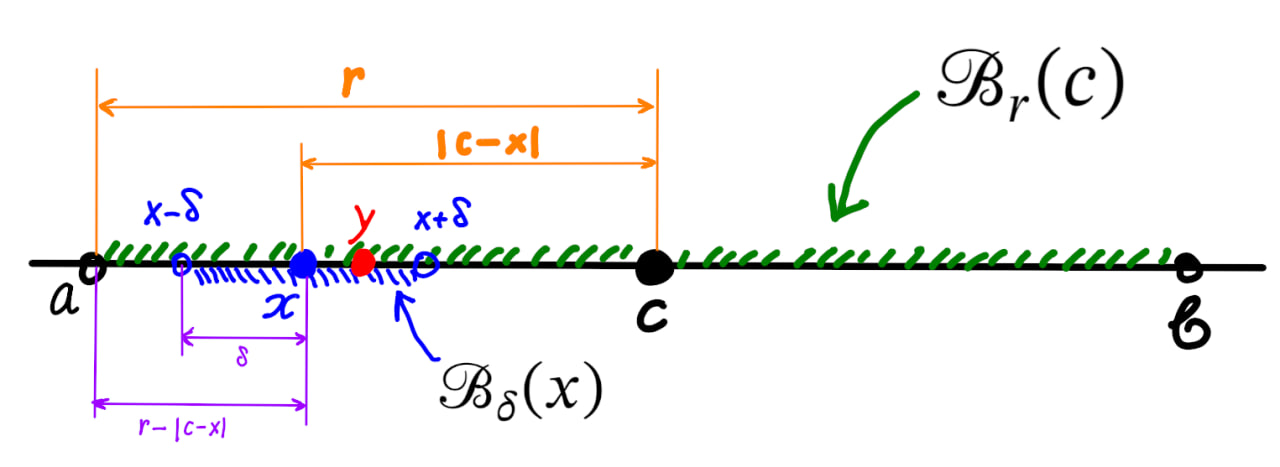
На зелёном интервале с центром в точке мы рассматриваем произвольную синюю точку и окружаем её синей окрестностью так, чтобы она целиком была в зелёном интервале.
Далее, используя неравенство треугольника[1], получаем
т.е. , а значит, , но это и показывает, что для любой точки , т.е. интервал — открыт. Это завершает доказательство.
Proof
Будем рассуждать от противного. Пусть не является открытым. Тогда это значит, что найдётся хотя бы одна точка , что для любого , . Но в таком случае это значит, что не является пустым множеством, что даёт противоречие. Это доказывает лемму.
Proof
(1) Пусть и пусть , тогда для какого-то , . Так как открыто, то найдётся такой , что , что и доказывает открытость множества
(2) Достаточно доказать, что пересечение двух открытых множеств открыто, а затем провести индукцию.
Если , то найдутся такие , что , . Тогда, если , то , что и доказывает открытость пересечения.
Proof
Действительно, имеем
и так как каждое из множеств, участвующее в объединениях, открыто, то по Lemma 3.1.4 мы получаем, что вся прямая и лучи , открытые множества.
Таким образом, окрестность радиуса — это частный случай окрестности.
Proof
(1) Пусть — открыто, тогда, согласно Definition 3.1.2, для любой точки существует такая -окрестность , что , т.е. полагая , что и доказывает необходимость.
(2) Пусть обладает тем свойством, что для любой точки существует такое открытое , что Рассмотрим множество
и покажем, что . Пусть , тогда существует хотя бы один , что , но так как , то , поэтому Пусть теперь , но тогда, согласно условию, существует такой , что , но тогда , потому что , т.е. , а значит,
Так как, согласно условию, каждый — открытое множество, то согласно Lemma 3.1.4, — открытое множество, что и требовалось доказать.
3.1.2Внутренние и внешние точки множества¶
Proof
Пусть , тогда существует такая окрестность , что , но согласно Definition 3.1.3, — открыто. Далее, для любой точки , мы получаем, что это же открытое множество есть её окрестность. Тогда для любой точки положим . Таким образом, все точки множества — внутренние, но это значит, что . Теперь, Proposition 3.1.1, мы завершаем доказательство.
Proof
Действительно, согласно Proposition 3.1.2, множество — открыто. Далее, если — открыто, то в силу Definition 3.1.2, каждая его точка — внутренняя, что и означает . Если же , то каждая точка множества является внутренней, но тогда, согласно Definition 3.1.4, это означает, что существует -окрестность этой точки которая целиком будет лежать в , т.е. согласно Definition 3.1.2 означает открытость .
3.1.3Замкнутые множества¶
Proof
Действительно, согласно Lemma 3.1.3, множество — открыто в , а так как , то значит, — замкнуто. Далее, согласно Corollary 3.1.1, множество — открыто, а так как , то значит, множество — замкнуто.
Proof
Пусть — какое-то семейство замкнутых множеств, тогда, согласно Definition 3.1.6, имеется семейство открытых множеств , что для любого
но согласно Lemma 3.1.4, множества , — открыты, что и завершает доказательство.
Proof
Действительно, имеем
согласно Corollary 3.1.1, множества — открыты, а по Lemma 3.1.4, множество — открыто, что и доказывает лемму.
Proof
Мы воспользуемся следующим фактом: тогда и только тогда, когда , где .
Поэтому нам достаточно показать, что
Если , то , а это значит, что существует такая окрестность , что , т.е. , а тогда это значит, что , поэтому
Если , то найдётся такая её окрестность , что , **т.е. ** , а это значит, что не может быть точкой прикосновения, т.е. , поэтому , что и доказывает утверждение.
Proof
Согласно Proposition 3.1.4, , а согласно Proposition 3.1.2, множество открыто, поэтому — замкнуто.
Proof
(1) Пусть — замкнуто, тогда найдётся какое-то открытое такое, что . Пусть , тогда , и тогда найдётся окрестность такая, что , потому что — открыто, т.е. Таким образом, получили, что если — замкнуто, то никакая точка не может быть точкой прикосновения для , т.е.
(2) Пусть , тогда если , то не может быть точкой прикосновения для , а это значит, что можно найти окрестность такую, что , иначе было бы точкой прикосновения. Итак, для любого , мы имеем окрестность такую, что . Рассмотрим теперь объединения всех таких окрестностей,
так как каждое открыто, то согласно Lemma 3.1.4, — открыто.
Пусть , тогда , а тогда , поэтому . Если , то , т.е. для любого , , т.е. , но это значит, что для любого , а тогда . Таким образом, , поэтому Это завершает доказательство леммы.