Дифференцируемость - The Hitchhiker's Guide to the Calculus Galaxy

Напомним, что векторное пространство $\mathbb{R}^n$ это просто набор $\{(x_1,\ldots, x_n)^\top\}$ столбцов, которые можно покомпонентно складывать и умножать на число. Выделяется особый набор таких столбцов $\mathbb{e} = \{\mathbf{e}_1, \ldots, \mathbf{e}_n\}$ , где $\mathbf{e}_1 = (1,0, \ldots, 0)^\top, \ldots, \mathbf{e}_n = (0,0,\ldots, 1)^\top$ . Множество таких столбцов называется стандартным базисом для $\mathbb{R}^n$ . Имеют место очевидные равенства, возьмём $\mathbf{x} = (x_1,\ldots, x_n)^\top \in \mathbb{R}^n$ , тогда ясно, что

\begin{pmatrix} x_1 \\ \vdots \\x_n \end{pmatrix} = x_1 \begin{pmatrix} 1 \\ \vdots \\ 0 \end{pmatrix} + \cdots + x_n \begin{pmatrix} 0 \\ \vdots \\1 \end{pmatrix}

Линейное отображение $\mathscr{L}:\mathbb{R}^n \to \mathbb{R}^m$ — это такое отображение, что $\mathscr{L}(\alpha \m{x} +\beta \m{y} ) = \alpha \mathscr{L}(\m{x}) +\beta \mathscr{L}(\m{y})$ , где $\m{x,y} \in \mathbb{R}^n$ , $\alpha, \beta \in \mathbb{R}.$

Любое линейное отображение $\mathscr{L}:\mathbb{R}^n \to \mathbb{R}^m$ удобно задавать матрицей $L$ . Так как оно линейно, то достаточно знать образы базисных векторов. Действительно, пусть

\mathscr{L}: \begin{pmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{pmatrix} \mapsto \begin{pmatrix} a_{11} \\ a_{21} \\ \vdots\\ a_{m1} \end{pmatrix}, \qquad \mathscr{L}: \begin{pmatrix} 0 \\ 1 \\ \vdots \\ 0 \end{pmatrix} \mapsto \begin{pmatrix} a_{12} \\ a_{22} \\ \vdots\\ a_{m2} \end{pmatrix}, \quad \ldots, \quad \mathscr{L}: \begin{pmatrix} 0 \\ 0 \\ \vdots \\ 1 \end{pmatrix} \mapsto \begin{pmatrix} a_{1n} \\ a_{2n} \\ \vdots\\ a_{mn} \end{pmatrix}

тогда матрица принимает вид

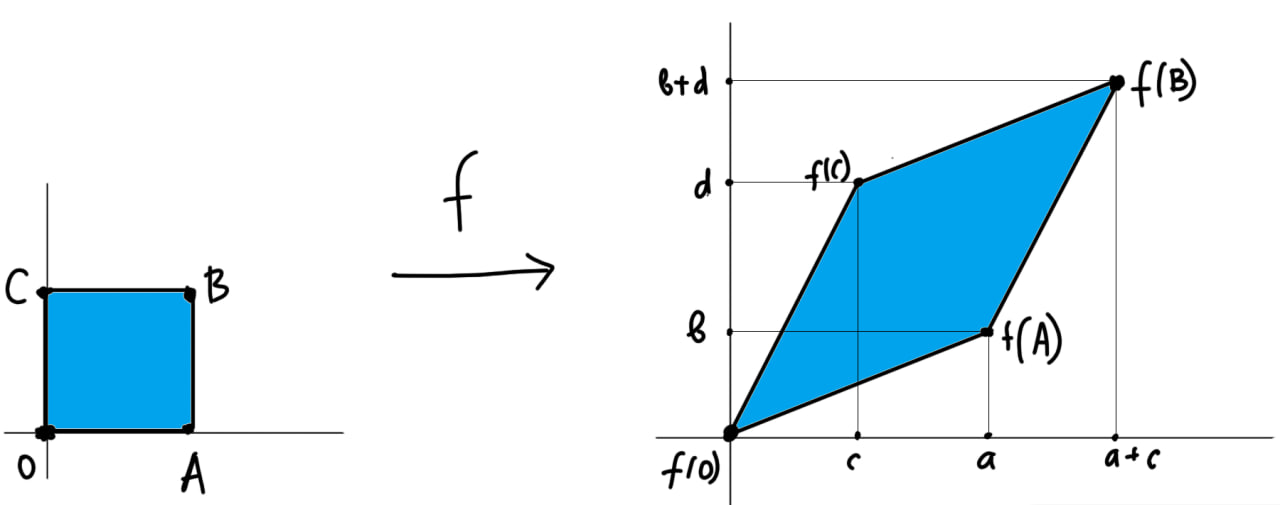
L = \begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \ldots& a_{mn} \end{pmatrix}

Линейное отображение f:\mathbb{R}^2 \to \mathbb{R}^2, которое задаётся матрицей A = \begin{pmatrix}
a & c \\
b & d
\end{pmatrix}. — Figure 1:Линейное отображение $f:\mathbb{R}^2 \to \mathbb{R}^2$ , которое задаётся матрицей $A = \begin{pmatrix} a & c \\ b & d \end{pmatrix}.$

Разумеется, не все отображения линейны. Однако некоторые из них локально очень похожи на линейные. Чтобы формализовать эту идею, вводят понятие дифференцируемости.

Definition 1

Пусть $\mathbb{R}^n$ , $\mathbb{R}^m$ — векторные пространства с евклидовой нормой $||?||$ , $\mathscr{U} \subseteq \mathbb{R}^n$ — открытое подмножество. Говорят, что отображение $F: \mathscr{U} \to \mathbb{R}^m$ дифференцируемо в точке $\m{x} \in \mathbb{R}^n$ , если существует такое линейное отображение (зависящее от точки $\m{x}$ ) $\mathrm{d}F_{\mathbb{x}}:\mathbb{R}^n \to \mathbb{R}^m$ , что

F(\m{x} + \m{h}) = F(\m{x}) + \mathrm{d}F_\m{x}(\m{h}) + o(||\m{h}||).

Если отображение дифференцируемо в каждой точке $\mathscr{U}$ , то говорят, что оно дифференцируемо на $\mathscr{U}$ .

Линейное отображение $\mathrm{d}F_\m{x}$ называется дифференциалом отображения в точке $\mathbb{x}$ .

Прежде всего, мы должны убедиться, что линейные отображения тоже дифференцируемы.

Proof

Действительно, так как $\mathscr{L}$ — линейное, то для любых $\m{x,h} \in \mathbb{R}^n$ ,

\mathscr{L}(\m{x}+\m{h}) = \mathscr{L}(\m{x}) + \mathscr{L}(\m{h}),

полагая теперь, что $\mathrm{d}\mathscr{L}_\mathbf{x}:=\mathscr{L}$ , и так как нулевая функция 0, очевидно, лежит в $o(||\m{h}||)$ , мы и получаем требуемое.

В дальнейшем нам понадобится следующая

Proof

Так как $|| \m{h} || = \sqrt{h_1^2 + \cdots + h^2_n}$ , то согласно неравенству (Equation),

\max_{1\le k \le n} |h_k| \le || \m{h} || \le \sqrt{n} \max_{1\le k \le n} |h_k|

поэтому если $||\m{h} || \to 0$ , то $|h_k| \to 0$ , что и доказывает требуемое.

Proof

Возьмём произвольный ненулевой вектор $\m{h} \in \mathbb{R}^n$ и рассмотрим выражение $F(\m{x}_0 + \m{h}) - F(\m{x}_0)$ , так как $F$ — дифференцируемо в $\m{x}_0$ , то

\lim_{\m{h} \to \m{0}} \frac{F(\m{x}_0 + \m{h}) - F(\m{x_0})}{|| \m{h} ||} = (\mathrm{d}F)_{\m{x}_0}(\m{h}) \in \mathbb{R}^m,

тогда

\begin{align*} \lim_{\m{h} \to \m{0}}( F(\m{x}_0 + \m{h}) - F(\m{x}_0) ) &=& \lim_{\m{h} \to \m{0}} \frac{F(\m{x}_0 + \m{h}) - F(\m{x_0})}{|| \m{h} ||} || \m{h}|| \\ &=& (\mathrm{d}F)_{\m{x}_0}(\m{h}) \lim_{\m{h} \to \m{0}} || \m{h} || \\ &=& 0, \end{align*}

но тогда $\lim_{\m{v} \to \m{x}_0}F(\m{v}) = F(\m{x}_0)$ но это и означает непрерывность $F.$ ^[1]

1Дифференцируемость функций от одной переменной.¶

Пусть $n=m=1$ , тогда любое линейное отображение $\mathscr{L}:\mathbb{R} \to \mathbb{R}$ имеет простой вид $\mathscr{L}(x) = kx$ , $k \in \mathbb{R}$ — фиксированное число, и $||\m{h}|| : = |h|$ — обыкновенный модуль. Тогда, согласно определению, функция $f:\mathbb{R} \to \mathbb{R}$ дифференцируема в точке $x_0$ , если существует такое число $k\in \mathbb{R}$ , что

f(x_0+h) = f(x_0)+kh + o(h), \qquad h \to 0.

Рассмотрим примеры.

Example 1

Пусть $f(x) = x^2$ , покажем, что она дифференцируема всюду. Действительно, имеем

\begin{align*} f(x+h) &=& (x+h)^2 \\ &=& x^2 + 2xh + h^2 \\ &=& f(x) + 2x \cdot h + o(|h|). \end{align*}

Таким образом, дифференциал определяется следующим образом: $\mathrm{d}f_{x_0} = 2x_0$ для любого $x_0 \in \mathbb{R}$ .

Это же равенство можно записать ещё так:

(x+h)^2 \approx x^2 + 2xh,

при этом, чем меньше будет $h$ , тем точнее будет результат. Например, $1.1^2 =1.21$ , а по нашей формуле $1.1^2 = (1+0.1)^2 \approx 1^2+ 2\cdot 1 \cdot 0.1 = 1.2.$

Example 2

Мы рассмотрим функцию уже от двух переменных $F: \mathbb{R}^2 \to \mathbb{R}$ , $F(x_1,x_2): = (x_1 + x_2)^2$ , где $\m{x} = (x_1, x_2)$ . Покажем, что она тоже всюду дифференцируема. Пусть $\m{h}= (h_1,h_2)$ , тогда получаем

\begin{align*} F(\m{x} + \m{h}) &=& F((x_1 +h_1) + (x_2 + h_2) ) \\ &=& ((x_1 +h_1) + (x_2 + h_2) )^2 \\ &=& ((x_1 + x_2) + (h_1 + h_2))^2 \\ &=& (x_1 + x_2)^2 + 2(x_1 + x_2)(h_1 + h_2) + (h_1 + h_2)^2 \\ &=& F(\mathbf{x}) + \begin{pmatrix} 2(x_1 + x_2) & 2(x_1 + x_2) \end{pmatrix} \begin{pmatrix} h_1 \\ h_2 \end{pmatrix} + o(||\m{h}||). \end{align*}

Прокомментируем, что тут написано. Во-первых, если $\m{h} \to 0$ , то, по Лемме Lemma 2, $h_1, h_2 \to 0$ . Мы должны показать, что $(h_1+h_2)^2 \in o(||\m{h}||)$ , т. е. $\lim_{h_1 \to 0, h_2 \to 0} \frac{(h_1 + h_2)^2}{\sqrt{h_1^2 + h_2^2}} = 0$ . Применим полярную систему координат $h_1 = \rho \cos \varphi$ , $h_2 = \rho \sin \varphi$ , тогда $\rho = \sqrt{h_1^2 + h_2^2} \to 0$ .

Имеем

\begin{align*} \lim_{h_1 \to, h_2 \to 0} \frac{(h_1 + h_2)^2}{\sqrt{h_1^2 + h_2^2}} &=& \lim_{\rho \to 0} \frac{\rho ^2 + 2\rho^2 \cos \varphi \sin \varphi }{\rho} \\ &=& \lim_{\rho \to 0} \rho \cdot \left(1 + \sin 2\varphi \right) \\ &=& 0, \end{align*}

поэтому $(h_1 + h_2)^2 \in o(||\m{h}||).$

Во-вторых, произведение $2(x_1 + x_2)(h_1 + h_2)$ можно записать в виде произведения матриц

\begin{pmatrix} 2(x_1 + x_2) &2(x_1 + x_2) \end{pmatrix} \begin{pmatrix} h_1 \\ h_2 \end{pmatrix} = 2(x_1 + x_2)(h_1+h_2),

таким образом, наше отображение $F$ — дифференцируемо, его дифференциал в точке $(a, b)$ задаётся матрицей размера $1\times 2$ :

\mathrm{d}F_{(a,b)} = \begin{pmatrix} 2(a+b) & 2(a+b) \end{pmatrix}.

Вернёмся к функциям от одной переменной.

Запись $f(x_0+h) = f(x_0)+kx_0 + o(h),$ $h \to 0$ означает также, что

k = \lim_{h \to 0} \frac{f(x_0 +h) - f(x_0)}{h}

таким образом, дифференцируемость функции равносильна существованию этого предела.

Нам нужно показать, что $\lim_{x \to x_0}f(x) = f(x_0)$ , так как значение $f(x_0)$ по определению определено. Пусть $x:=x_0 +h$ , тогда если $h \to 0$ , то $x \to x_0$ и тогда из определения производной в точке $x_0$ следует, что существует предел

f'(x_0) = \lim_{x\to x_0} \frac{f(x) - f(x_0)}{x-x_0}.

Имеем

f(x) - f(x_0) = \frac{f(x) - f(x_0)}{x-x_0}(x-x_0),

тогда

\begin{align*} \lim_{x \to x_0} (f(x) - f(x_0)) &=& \lim_{x \to x_0}\frac{f(x) - f(x_0)}{x-x_0}(x-x_0) \\ &=& f'(x_0) \lim_{x \to x_0}(x-x_0) \\ &=& 0, \end{align*}

т. е. $\lim_{x \to x_0} f(x) = f(x_0)$ , что и означает её непрерывность.\

2Типичные недифференцируемые функции¶

Позже мы покажем, что если функция дифференцируема в точке, то к ней можно провести касательную в этой точке. Физически дифференцируемость функции от одной переменной означает, что скорость процесса (который описывается заданной функцией) меняется непрерывно от точки к точке, т. е. не может быть мгновенного скачка скорости в какой-то точке.

Example 3

Рассмотрим функцию $f(x) = |x|$ , покажем, что она недифференцируема в точке $x_0 =0$ .

График функции $f(x) = |x|.$

Рассмотрим предел

\begin{align*} \lim_{x \to 0}\frac{f(x) - f(0)}{x - 0} &=& \lim_{x \to 0} \frac{|x| - 0}{x-0} \\ &=&\lim_{x \to 0} \frac{|x|}{x}\\ &=& \lim_{x \to 0}\mathrm{sign}(x), \end{align*}

где $\mathrm{sign}(x) : = \begin{cases} 1, & x > 0, \\ 0, & x =0, \\ -1 , & x <0, \end{cases}$ но эта функция не непрерывна в точке $x_0$ , а значит, и нет предела $\lim_{x \to 0}\frac{f(x) - f(0)}{x - 0}$ , что и означает, что эта функция недифференцируема в точке $x_0 = 0.$

Красным показан график функции f(x) = |x|, а синим — график функции g(x) = \mathrm{sign}(x), мы видим, что g(x) делает резкий скачок в точке 0, что и означает, что функция f(x) недифференцируема. — Красным показан график функции $f(x) = |x|$ , а синим — график функции $g(x) = \mathrm{sign}(x)$ , мы видим, что $g(x)$ делает резкий скачок в точке 0, что и означает, что функция $f(x)$ недифференцируема.

Example 4

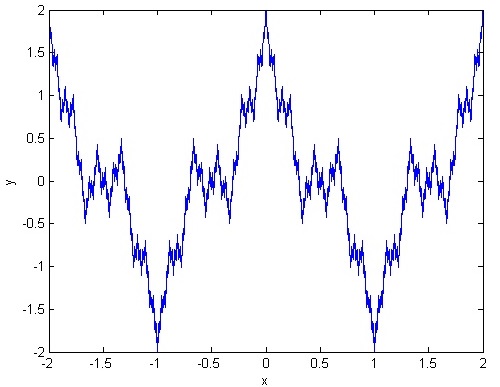
Одним из самых ярких контрпримеров является функция Вейерштрасса — всюду непрерывная, но нигде не дифференцируемая функция. Аналитически она записывается следующим образом:

f(x) = \sum_{n=0}^{\infty} {a^n \cos(b^n \pi x)},

где $0 < a < 1, \; b$ — положительное нечётное целое и

ab > 1 + \frac{3 \pi}{2}

Схематично график функции показан на Рис. Figure 4.

Простыми словами, функция Вейерштрасса резко меняет своё направление в каждой точке, поэтому не может быть дифференцируемой, но она также всюду непрерывна как предел равномерно сходящихся всюду непрерывных частичных сумм.

Proof

(1) Это сразу следует из того, что предел суммы — это сумма пределов.

Footnotes¶

мы тут положили, что $\m{v}: = \m{x}_0 +\m{h}$ .
↩

Анализ в ℝⁿ

o-символика Ландау и бесконечно малые функции

Анализ в ℝⁿ

Геометрический смысл дифференциала функции