Геометрический смысл дифференциала функции - The Hitchhiker's Guide to the Calculus Galaxy

Skip to article frontmatter Skip to article content

Мы начнём с рассмотрения функции от одной переменной.

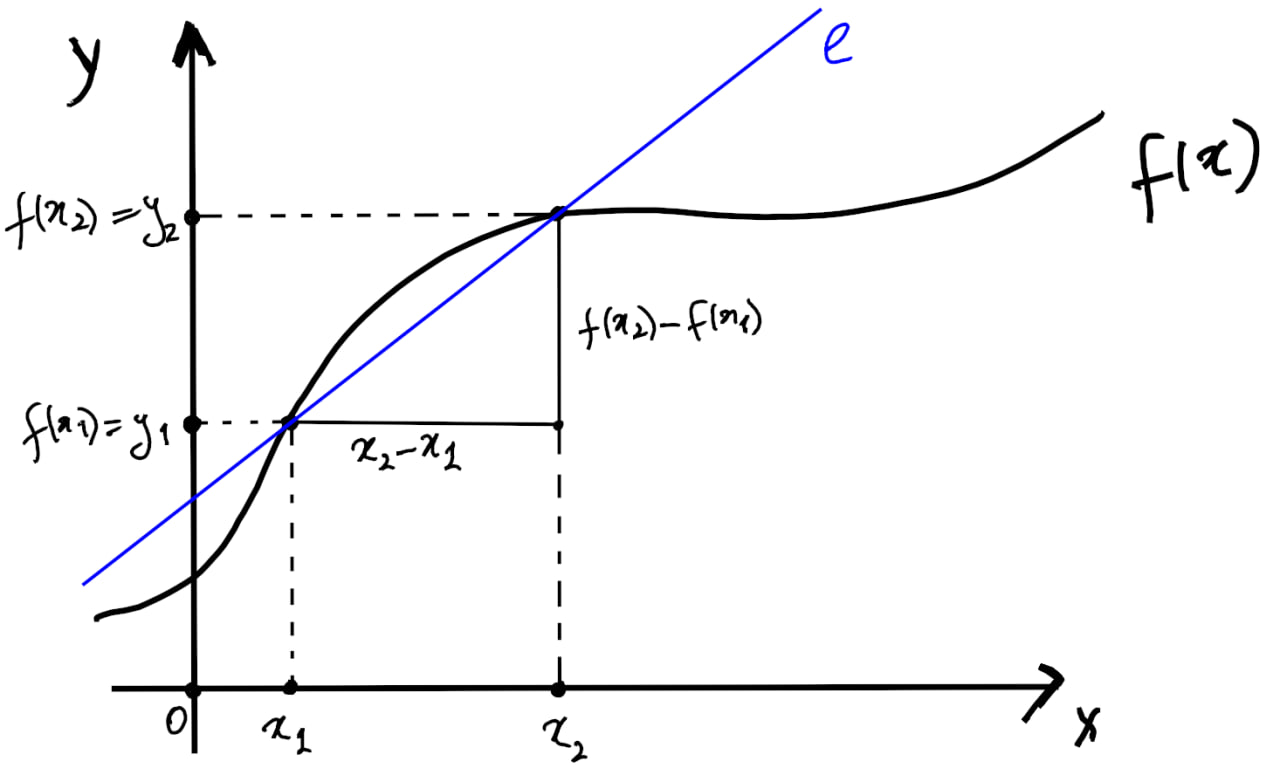
Прямая \ell, проходящая через точки (x_1,y_1), (x_2,y_2), где y_1 = f(x_1), y_2 = f(x_2) — Прямая $\ell$ , проходящая через точки $(x_1,y_1)$ , $(x_2,y_2)$ , где $y_1 = f(x_1)$ , $y_2 = f(x_2)$

Proof

Рассматриваемая прямая задаётся уравнением

y = \frac{f(x_2) - f(x_1)}{x_2 - x_1}(x-x_1) +y_1,

поэтому

k(x_2) = \frac{f(x_2) - f(x_1)}{x_2 - x_1}.

Тогда из определения производной следует, что

\lim_{x_2 \to x_1}k(x_2) = f'(x_1).

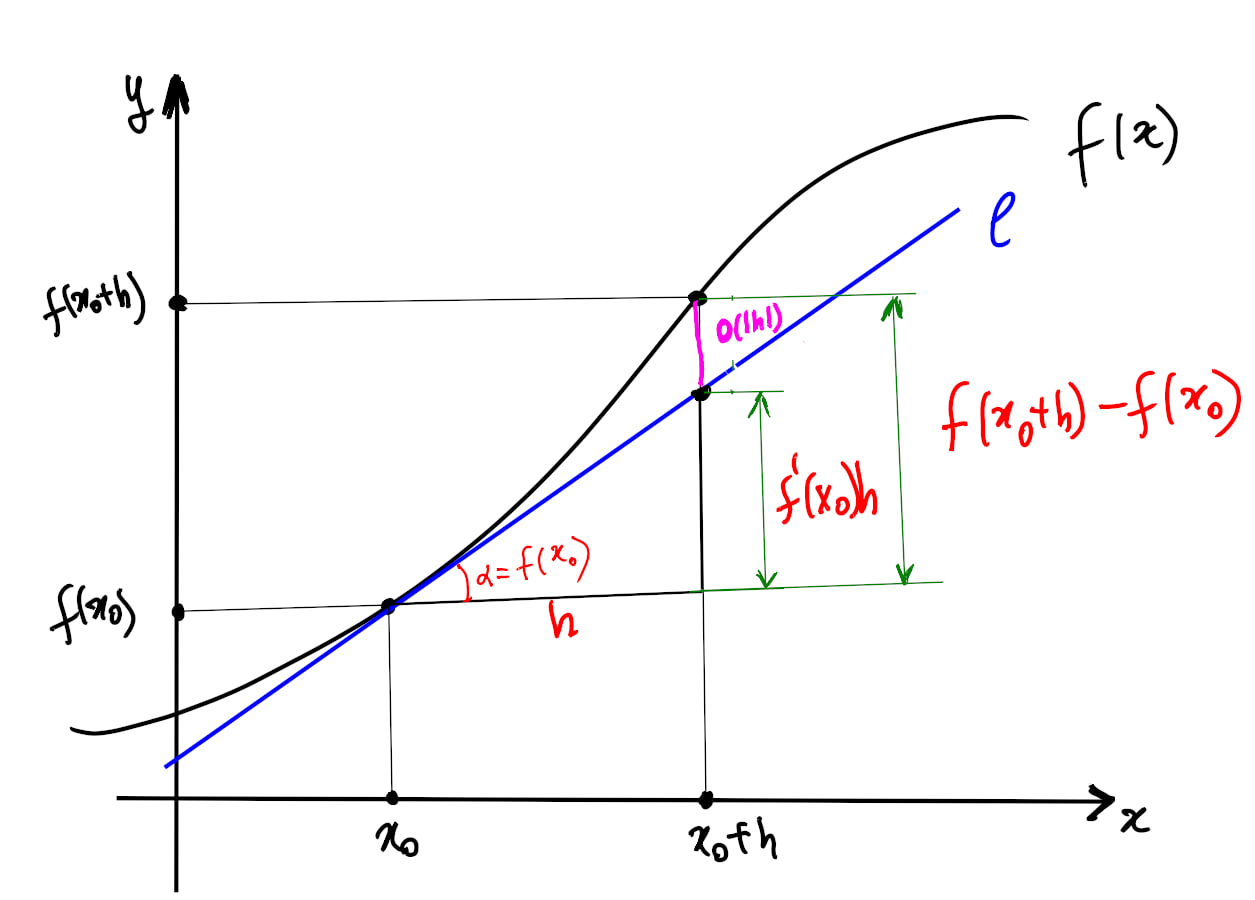
Таким образом, если функция f(x) дифференцируема в точке x_0, то её можно приблизить линейной функцией f'(x_0)(x-x_0) +f(x_0), при этом o(|h|) показывает, насколько далеко это приближение. — Таким образом, если функция $f(x)$ дифференцируема в точке $x_0$ , то её можно приблизить линейной функцией $f'(x_0)(x-x_0) +f(x_0)$ , при этом $o(|h|)$ показывает, насколько далеко это приближение.

Анализ в ℝⁿ

Дифференцируемость

Анализ в ℝⁿ

Частные производные и явная формула для дифференциала