Понятие определённого интеграла восходит ещё к Архимеду. Мы рассмотрим неформальное введение, где объясним суть проблемы.
Пусть дана функция , которая непрерывна на отрезке . Будем писать и будем считать, что функция на этом отрезке принимает только положительные значения. Рассмотрим фигуру (см. рис.Figure 1), ограниченную кривой , двумя ординатами , и отрезком оси Подобные фигуры называются криволинейными трапециями.
Рассмотрим теперь задачу о нахождении площади плоской криволинейной трапеции (см. рис.Figure 1)
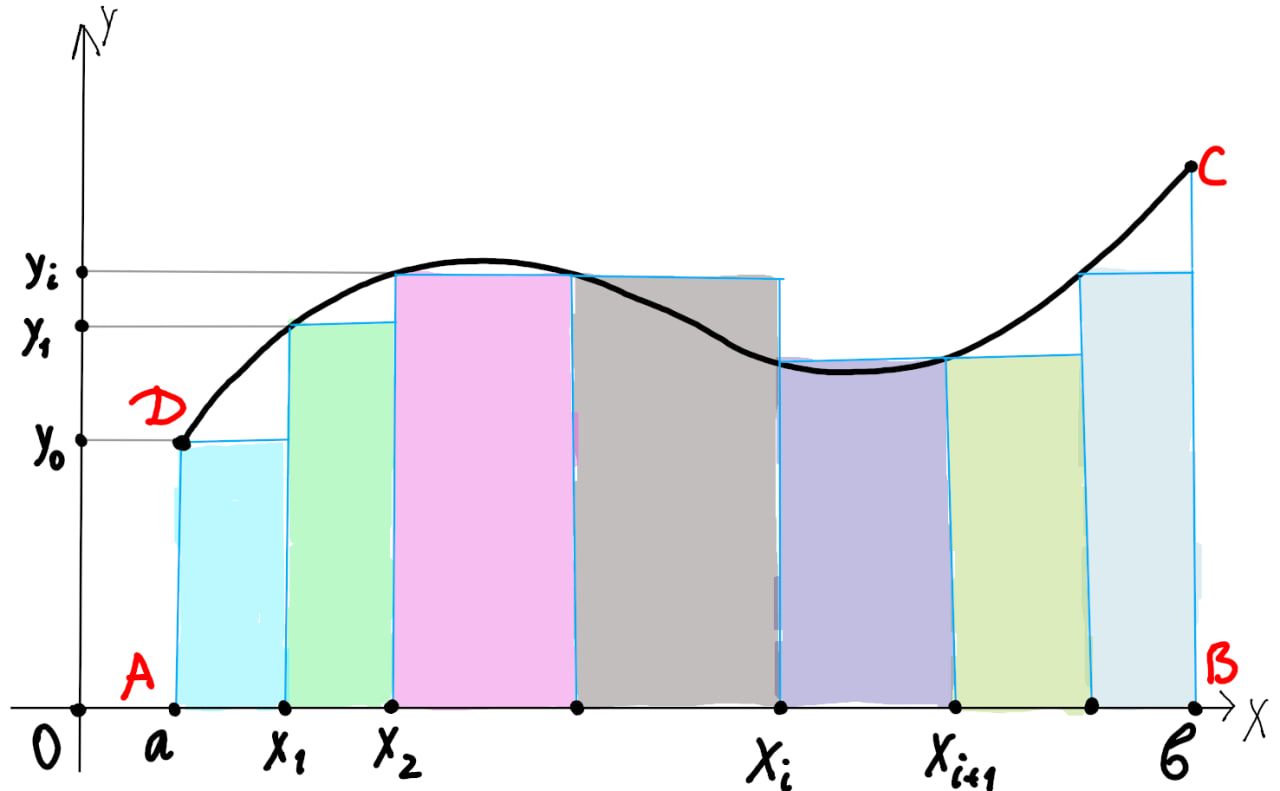
Figure 1:Площадь фигуры примерно равна сумме площадей разноцветных прямоугольников, и чем их больше, тем точнее будет ответ.
Разделим основание нашей фигуры произвольным образом на части и проведём ординаты, соответствующие точкам деления; тогда криволинейная трапеция разобьётся на ряд полосок.
Заменим теперь приближённо каждую полоску некоторым прямоугольником, основание которого то же, что и у полоски, а высота совпадает с одной из ординат полоски. Таким образом, криволинейная фигура заменится некоторой ступенчатой фигурой, составленной из отдельных прямоугольников.
Обозначим абсциссы точек деления через
Будем нумеровать прямоугольники числами и пусть — площадь -го прямоугольника. Ясно, что , где
Тогда приближённое значение площади криволинейной трапеции равно
Тогда можно предположить, что при убывании всех к нулю мы будем получать более точное значение, т.е. другими словами мы хотим сказать, что точное значение площади это следующий предел
Для обозначения предела такой суммы вида и был Лейбницем введён символ интеграла, т.е.