В этой главе мы познакомимся с понятием интеграла. Мы будем развивать теорию интегрирования для функций от одной переменной. Прежде всего, мы напомним важные факты из дифференциального исчисления функции от одной переменной.
Нам понадобится напоминание понятия дифференциала и некоторое важное для дальнейшего соглашение.
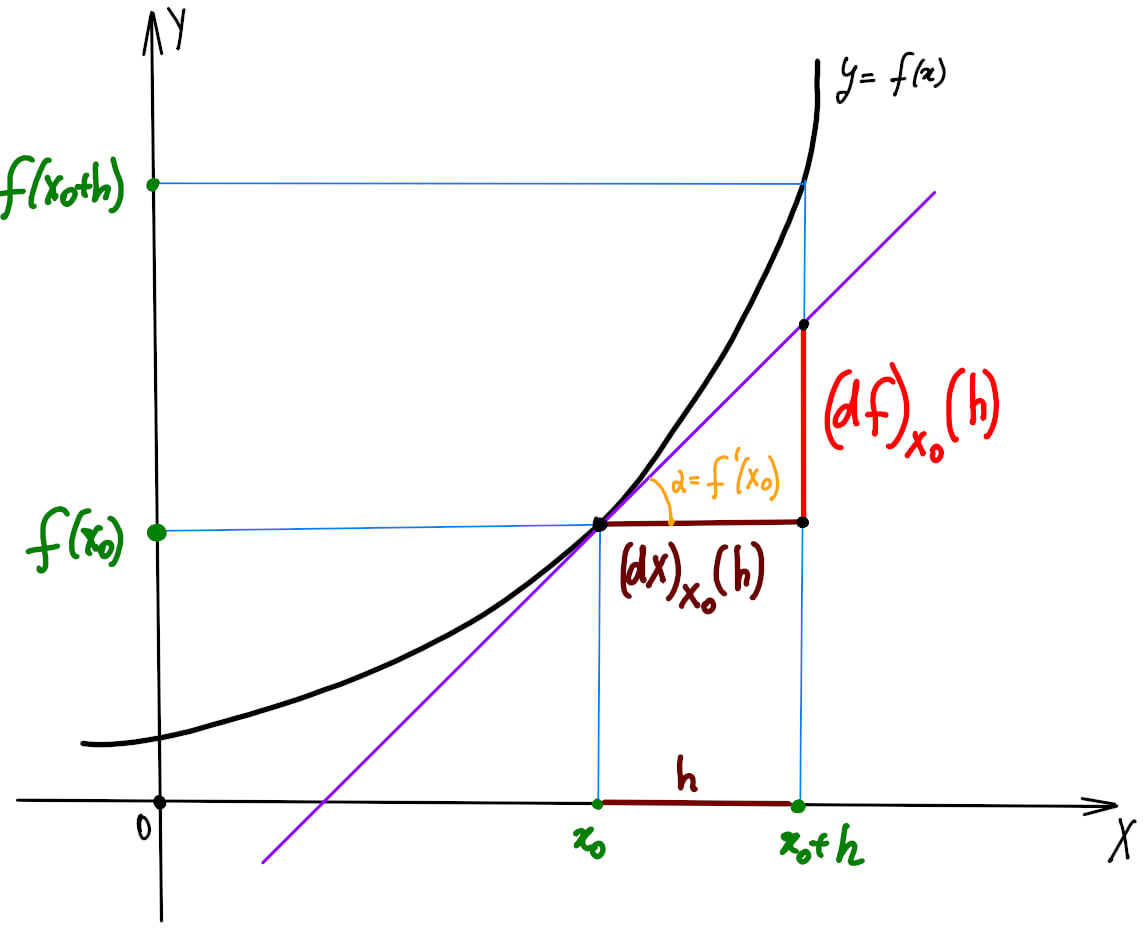
Пусть имеется функция f : R → R f:\mathbb{R} \to \mathbb{R} f : R → R x 0 x_0 x 0 ( d f ) x 0 : R → R (\mathrm{d}f)_{x_0}: \mathbb{R} \to \mathbb{R} ( d f ) x 0 : R → R
f ( x 0 + h ) = f ( x 0 ) + ( d f ) x 0 ( h ) + o ( ∣ h ∣ ) , h → 0.
f(x_0 + h) = f(x_0) + (\mathrm{d}f)_{x_0}(h) + o(|h|), \qquad h \to 0. f ( x 0 + h ) = f ( x 0 ) + ( d f ) x 0 ( h ) + o ( ∣ h ∣ ) , h → 0. При этом, как мы уже знаем, это линейное отображение ( d f ) x 0 (\mathrm{d}f)_{x_0} ( d f ) x 0 f f f x 0 x_0 x 0
( d f ) x 0 ( h ) : = f ′ ( x 0 ) ⋅ h ,
(\mathrm{d}f)_{x_0}(h): = f'(x_0)\cdot h, ( d f ) x 0 ( h ) := f ′ ( x 0 ) ⋅ h , где мы от h ∈ R h \in \mathbb{R} h ∈ R h → 0 h\to 0 h → 0 ( d f ) x 0 ( h ) → 0. (\mathrm{d}f)_{x_0}(h) \to 0. ( d f ) x 0 ( h ) → 0.
Рассмотрим теперь функцию y ( x ) = x y(x) = x y ( x ) = x
( d x ) x 0 ( h ) = ( x ′ ( x 0 ) ) ⋅ h
(\mathrm{d}x)_{x_0}(h) = (x'(x_0))\cdot h ( d x ) x 0 ( h ) = ( x ′ ( x 0 )) ⋅ h и так как x ′ = 1 x' = 1 x ′ = 1 ( d x ) x 0 ( h ) = h (\mathrm{d}x)_{x_0}(h) = h ( d x ) x 0 ( h ) = h
( d f ) x 0 ( h ) = f ′ ( x 0 ) ⋅ h = f ′ ( x 0 ) ⋅ ( d x ) x 0 ( h ) .
(\mathrm{d}f)_{x_0}(h) = f'(x_0) \cdot h = f'(x_0) \cdot (\mathrm{d}x)_{x_0}(h). ( d f ) x 0 ( h ) = f ′ ( x 0 ) ⋅ h = f ′ ( x 0 ) ⋅ ( d x ) x 0 ( h ) . Тогда мы можем сократить эту формулу следующим образом
d f = f ′ ⋅ d x . \boxed{
\mathrm{d}f = f'\cdot \mathrm{d}x.
} d f = f ′ ⋅ d x . Нужно понимать, что полученная формула это всего лишь соглашение!!! Ведь эта формула должна пониматься как это написано выше, т.е. ( d f ) x 0 ( h ) = f ′ ( x 0 ) ⋅ ( d x ) x 0 ( h ) . (\mathrm{d}f)_{x_0}(h) = f'(x_0) \cdot (\mathrm{d}x)_{x_0}(h). ( d f ) x 0 ( h ) = f ′ ( x 0 ) ⋅ ( d x ) x 0 ( h ) .
Рассмотрим теперь R n \mathbb{R}^n R n e = ( e 1 , … , e n ) \mathbb{e} = (\m{e}_1,\ldots, \m{e}_n) e = ( e 1 , … , e n ) h = ( h 1 , … , h n ) ⊤ ∈ R n \m{h} = (h_1,\ldots, h_n)^\top \in \mathbb{R}^n h = ( h 1 , … , h n ) ⊤ ∈ R n h = h 1 e 1 + ⋯ + h n e n . \m{h} = h_1\m{e}_1 + \cdots + h_n \m{e}_n. h = h 1 e 1 + ⋯ + h n e n .
Рассмотрим координатные функции
x 1 , … , x n : R n → R , x i ( h ) : = h i , 1 ≤ i ≤ n .
x_1,\ldots, x_n:\mathbb{R}^n \to \mathbb{R}, \qquad x_i(\m{h}): = h_i, \quad 1 \le i \le n. x 1 , … , x n : R n → R , x i ( h ) := h i , 1 ≤ i ≤ n . Тогда их дифференциалы ( d x 1 , … , d x n ) (\mathrm{d}x_1, \ldots, \mathrm{d}x_n) ( d x 1 , … , d x n ) ( R n ) ∗ (\mathbb{R}^n)^* ( R n ) ∗
( d x i ) ( e j ) = δ i , j : = { 1 , i = j , 0 , i ≠ j .
(\mathrm{d}x_i)(\m{e}_j) = \delta_{i,j}: = \begin{cases}
1, & i = j, \\
0, & i \ne j.
\end{cases} ( d x i ) ( e j ) = δ i , j := { 1 , 0 , i = j , i = j . Тогда, если f : R n → R f:\mathbb{R}^n \to \mathbb{R} f : R n → R a \m{a} a
∇ a f = ∂ f ∂ x 1 ∣ a ⋅ d x 1 + ⋯ + ∂ f ∂ x n ∣ a ⋅ d x n . \boxed{
\nabla_\m{a} f = \left.\frac{\partial f}{\partial x_1}\right|_\m{a} \cdot \mathrm{d}x_1 + \cdots + \left.\frac{\partial f}{\partial x_n}\right|_\m{a} \cdot \mathrm{d}x_n.
} ∇ a f = ∂ x 1 ∂ f ∣ ∣ a ⋅ d x 1 + ⋯ + ∂ x n ∂ f ∣ ∣ a ⋅ d x n . Действительно, имеем
( ∇ a f ) ( h ) = ∂ f ∂ x 1 ∣ a ⋅ d x 1 ( h ) + ⋯ + ∂ f ∂ x n ∣ a ⋅ d x n ( h ) = ∂ f ∂ x 1 ∣ a ⋅ h 1 + ⋯ + ∂ f ∂ x n ∣ a ⋅ h n , \begin{align*}
(\nabla_\m{a} f) (\m{h}) &= \left.\frac{\partial f}{\partial x_1}\right|_\m{a} \cdot \mathrm{d}x_1(\m{h}) + \cdots + \left.\frac{\partial f}{\partial x_n}\right|_\m{a} \cdot \mathrm{d}x_n (\m{h}) \\
&= \left.\frac{\partial f}{\partial x_1}\right|_\m{a} \cdot h_1 + \cdots + \left.\frac{\partial f}{\partial x_n}\right|_\m{a} \cdot h_n ,
\end{align*} ( ∇ a f ) ( h ) = ∂ x 1 ∂ f ∣ ∣ a ⋅ d x 1 ( h ) + ⋯ + ∂ x n ∂ f ∣ ∣ a ⋅ d x n ( h ) = ∂ x 1 ∂ f ∣ ∣ a ⋅ h 1 + ⋯ + ∂ x n ∂ f ∣ ∣ a ⋅ h n , что и есть определение дифференциала фукнции.
Это как раз и показывает, что градиент функции есть элемент двойственного пространства, т.е. градиент — это ковектор (=функционал), а не вектор!
Выражение вида
f 1 d x 1 + ⋯ + f n d x n ,
f_1 \mathrm{d}x_1 + \cdots + f_n \mathrm{d}x_n, f 1 d x 1 + ⋯ + f n d x n , где f 1 , … , f n : R n → R f_1,\ldots, f_n:\mathbb{R}^n \to \mathbb{R} f 1 , … , f n : R n → R линейной дифференциальной формой или 1-формой , и обычно они обозначаются через ω, а пространство всех линейных дифференциальных форм на R n \mathbb{R}^n R n Ω 1 ( R n ) . \Omega^1(\mathbb{R}^n). Ω 1 ( R n ) .
Дифференциал функции всюду дифференцируемой функции как раз и есть пример дифференциальной формы. Например, пусть f ( x 1 , x 2 ) = x 1 3 − 2 x 1 x 2 + 3 x 2 2 f(x_1,x_2) = x_1^3 - 2x_1x_2 + 3x_2^2 f ( x 1 , x 2 ) = x 1 3 − 2 x 1 x 2 + 3 x 2 2 R 2 \mathbb{R}^2 R 2
∂ f ∂ x 1 = 3 x 1 2 − 2 x 2 , ∂ f ∂ x 2 = − 2 x 1 + 6 x 2 , \begin{align*}
\frac{\partial f}{\partial x_1} &= 3x_1^2 - 2x_2, \\
\frac{\partial f}{\partial x_2} &= - 2x_1 + 6x_2,
\end{align*} ∂ x 1 ∂ f ∂ x 2 ∂ f = 3 x 1 2 − 2 x 2 , = − 2 x 1 + 6 x 2 , Поэтому, учитывая ((1)
∇ f = ( 3 x 1 2 − 2 x 2 ) d x 1 + ( − 2 x 1 + 6 x 2 ) d x 2 .
\nabla f = (3x_1^2-2x_2)\mathrm{d}x_1 + (-2x_1 + 6x_2) \mathrm{d}x_2. ∇ f = ( 3 x 1 2 − 2 x 2 ) d x 1 + ( − 2 x 1 + 6 x 2 ) d x 2 .