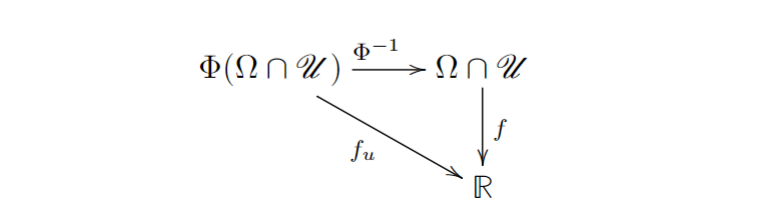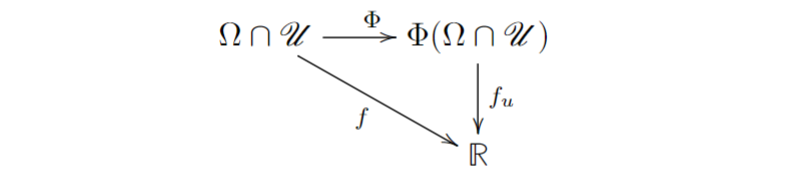Рассмотрим отображение
Φ : R n + m → R n + m , ( x 1 ⋮ x m x m + 1 ⋮ x n + m ) ↦ ( φ 1 ( x 1 , … , x n + m ) ⋮ φ m ( x 1 , … , x n + m ) x m + 1 ⋮ x n + m )
\Phi: \mathbb{R}^{n+m} \to \mathbb{R}^{n+m}, \qquad \begin{pmatrix}
x_1 \\ \vdots \\ x_m \\ x_{m+1} \\ \vdots \\ x_{n+m}
\end{pmatrix} \mapsto \begin{pmatrix}
\varphi_1(x_1,\ldots, x_{n+m}) \\
\vdots \\
\varphi_m(x_1,\ldots, x_{n+m}) \\
x_{m+1} \\ \vdots \\x_{n+m}
\end{pmatrix} Φ : R n + m → R n + m , ⎝ ⎛ x 1 ⋮ x m x m + 1 ⋮ x n + m ⎠ ⎞ ↦ ⎝ ⎛ φ 1 ( x 1 , … , x n + m ) ⋮ φ m ( x 1 , … , x n + m ) x m + 1 ⋮ x n + m ⎠ ⎞ согласно условиям, оно непрерывно дифференцируемо в окрестности W \mathscr{W} W a \m{a} a
Сделаем теперь замену переменных
u 1 = φ 1 ( x 1 , … , x n + m ) ⋮ ⋮ u m = φ m ( x 1 , … , x n + m ) u m + 1 = x m + 1 ⋮ ⋮ u m + n = x m + n \begin{matrix}
u_1 & = & \varphi_1(x_1,\ldots, x_{n+m}) \\
\vdots & & \vdots\\
u_m & = & \varphi_m(x_1,\ldots, x_{n+m}) \\
u_{m+1} &=& x_{m+1} \\
\vdots && \vdots \\
u_{m+n} &=& x_{m+n}
\end{matrix} u 1 ⋮ u m u m + 1 ⋮ u m + n = = = = φ 1 ( x 1 , … , x n + m ) ⋮ φ m ( x 1 , … , x n + m ) x m + 1 ⋮ x m + n Если нужно, то, перенумеровав переменные, можно считать, что из условия о ранге матрицы вытекает
d e t ( ∂ φ 1 ∂ x 1 ( x ) … ∂ φ 1 ∂ x m ( x ) ⋮ ⋱ ⋮ ∂ φ m ∂ x 1 ( x ) … ∂ φ m ∂ x m ( x ) ) ≠ 0.
\mathrm{det} \begin{pmatrix}
\dfrac{\partial \varphi_1}{\partial x_{1}}(\m{x}) &\ldots& \dfrac{\partial \varphi_1}{\partial x_{m}}(\m{x}) \\
\vdots & \ddots & \vdots \\
\dfrac{\partial \varphi_m}{\partial x_{1}}(\m{x}) &\ldots & \dfrac{\partial \varphi_m}{\partial x_{m}}(\m{x})
\end{pmatrix} \ne 0. det ⎝ ⎛ ∂ x 1 ∂ φ 1 ( x ) ⋮ ∂ x 1 ∂ φ m ( x ) … ⋱ … ∂ x m ∂ φ 1 ( x ) ⋮ ∂ x m ∂ φ m ( x ) ⎠ ⎞ = 0. Тогда по теореме об обратном отображении Theorem 1 U ⊆ W \mathscr{U} \subseteq \mathscr{W} U ⊆ W a . \m{a}. a . ψ i : V → R \psi_i: \mathscr{V} \to \mathbb{R} ψ i : V → R 1 ≤ i ≤ n + m 1\le i \le n+m 1 ≤ i ≤ n + m V \mathscr{V} V Φ ( a ) \Phi(\m{a}) Φ ( a ) (2)
x 1 = ψ 1 ( u 1 , … , u m ) ⋮ ⋮ x n + m = ψ n + m ( u 1 , … , u m ) \begin{matrix}
x_1 & = & \psi_1(u_1,\ldots, u_{m}) \\
\vdots & & \vdots\\
x_{n+m} & = & \psi_{n+m}(u_1,\ldots, u_m)
\end{matrix} x 1 ⋮ x n + m = = ψ 1 ( u 1 , … , u m ) ⋮ ψ n + m ( u 1 , … , u m ) $$
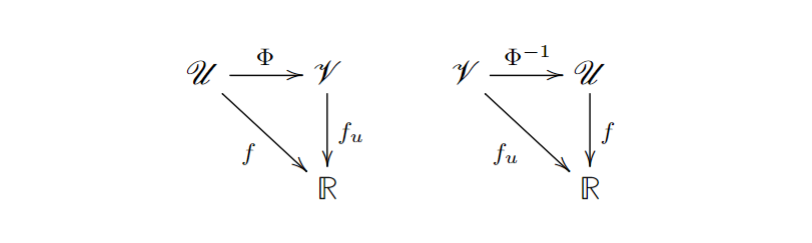
В итоге, мы получаем две коммутативные диаграммы
т.е.,
f u ( u 1 , … , u n + m ) : = f ( φ 1 ( x 1 , … , x n + m ) , … , φ m ( x 1 , … , x n + m ) , x m + 1 , … , x m + n ) ,
f_u(u_1, \ldots, u_{n+m}) := f(\varphi_1(x_1,\ldots, x_{n+m}), \ldots, \varphi_m(x_1,\ldots, x_{n+m}), x_{m+1},\ldots, x_{m+n}), f u ( u 1 , … , u n + m ) := f ( φ 1 ( x 1 , … , x n + m ) , … , φ m ( x 1 , … , x n + m ) , x m + 1 , … , x m + n ) , и
f ( x 1 , … , x n + m ) = f u ( ψ 1 ( u 1 , … , ψ m ) , … , ψ n + m ( u 1 , … , u m ) ) .
f(x_1,\ldots, x_{n+m})= f_u(\psi_1(u_1,\ldots, \psi_m), \ldots, \psi_{n+m}(u_1,\ldots, u_m)). f ( x 1 , … , x n + m ) = f u ( ψ 1 ( u 1 , … , ψ m ) , … , ψ n + m ( u 1 , … , u m )) . Тогда, если мы ограничимся рассмотрением точек на множестве Ω, то во-первых, мы получаем, что
Φ ( Ω ) = { ( u 1 , … , u n + m ) ∈ U : u 1 = 0 , … , u m = 0 } ,
\Phi(\Omega) = \{(u_1,\ldots, u_{n+m}) \in \mathscr{U}\, : \, u_1=0,\ldots, u_m=0\}, Φ ( Ω ) = {( u 1 , … , u n + m ) ∈ U : u 1 = 0 , … , u m = 0 } , во-вторых мы получаем функцию уже от n n n f u ( 0 , … , 0 , u m + 1 , … , u m + n ) f_u(0,\ldots, 0, u_{m+1},\ldots, u_{m+n}) f u ( 0 , … , 0 , u m + 1 , … , u m + n )
Далее, из диаграммы
следует, что при y ∈ Φ ( Ω ∩ U ) \m{y} \in \Phi(\Omega \cap \mathscr{U}) y ∈ Φ ( Ω ∩ U ) Φ − 1 \Phi^{-1} Φ − 1
Φ − 1 : ( 0 ⋮ 0 u m + 1 ⋮ u m + n ) ↦ ( 0 ⋮ 0 x m + 1 ⋮ x m + n ) ,
\qquad \Phi^{-1} : \begin{pmatrix}
0\\
\vdots \\
0\\
u_{m+1} \\
\vdots \\
u_{m+n}
\end{pmatrix} \mapsto \begin{pmatrix}
0\\
\vdots \\
0\\
x_{m+1} \\
\vdots \\
x_{m+n}
\end{pmatrix}, Φ − 1 : ⎝ ⎛ 0 ⋮ 0 u m + 1 ⋮ u m + n ⎠ ⎞ ↦ ⎝ ⎛ 0 ⋮ 0 x m + 1 ⋮ x m + n ⎠ ⎞ , а так как u m + 1 = x m + 1 , … , u m + n = x n + m u_{m+1} = x_{m+1}, \ldots, u_{m+n} =x_{n+m} u m + 1 = x m + 1 , … , u m + n = x n + m
f u ( 0 , … , 0 , u m + 1 , … , u m + n ) = f ( 0 , … , 0 , x m + 1 , … , x n + m ) ∘ Φ − 1 .
f_u(0,\ldots, 0, u_{m+1},\ldots, u_{m+n}) = f(0,\ldots, 0, x_{m+1}, \ldots, x_{n+m}) \circ \Phi^{-1}. f u ( 0 , … , 0 , u m + 1 , … , u m + n ) = f ( 0 , … , 0 , x m + 1 , … , x n + m ) ∘ Φ − 1 . Но тогда Φ ( a ) \Phi(\m{a}) Φ ( a ) f u ( 0 , … , 0 , u m + 1 , … , u m + n ) f_u(0,\ldots, 0, u_{m+1},\ldots, u_{m+n}) f u ( 0 , … , 0 , u m + 1 , … , u m + n ) Theorem 1
∂ f u ∂ u m + 1 ( Φ ( a ) ) = ⋯ = ∂ f u ∂ u m + n ( Φ ( a ) ) = 0.
\dfrac{\partial f_u}{\partial{u_{m+1}}}(\Phi(\m{a})) = \cdots = \dfrac{\partial f_u}{\partial{u_{m+n}}}(\Phi(\m{a})) = 0. ∂ u m + 1 ∂ f u ( Φ ( a )) = ⋯ = ∂ u m + n ∂ f u ( Φ ( a )) = 0. Это значит, что в точке Φ ( a ) \Phi(\m{a}) Φ ( a )
( d f u ) Φ ( a ) = ( λ 1 … λ m 0 … 0 ) .
(\mathrm{d}f_u)_{\Phi(\m{a})} = \begin{pmatrix}
\lambda_1 & \ldots & \lambda_m & 0 & \ldots & 0
\end{pmatrix}. ( d f u ) Φ ( a ) = ( λ 1 … λ m 0 … 0 ) . Наконец, из диаграммы
и из теоремы о композиции дифференциалов Theorem 1
( d f ) a = ( d f u ) Φ ( a ) ⋅ ( d Φ ) a = ( λ 1 … λ m 0 … 0 ) ( ∂ φ 1 ∂ x 1 ( a ) … ∂ φ 1 ∂ x m ( a ) ∂ φ 1 ∂ x m + 1 ( a ) … ∂ φ 1 ∂ x m + n ( a ) ⋮ ⋱ ⋮ ⋮ ⋱ ⋮ ∂ φ m ∂ x 1 ( a ) … ∂ φ m ∂ x m ( a ) ∂ φ n ∂ x m + 1 ( a ) … ∂ φ m ∂ x m + n ( a ) 0 … 0 1 … 0 ⋮ ⋱ ⋮ ⋮ ⋱ ⋮ 0 … 0 0 … 1 ) = λ 1 ( d φ 1 ) a + … + λ m ( d φ m ) a , \begin{align*}
(\mathrm{d}f)_\m{a} &= (\mathrm{d}f_u)_{\Phi(\m{a})} \cdot (\mathrm{d}\Phi)_{\m{a}} \\
&= \begin{pmatrix}
\lambda_1 & \ldots & \lambda_m & 0 & \ldots 0
\end{pmatrix} \begin{pmatrix}
\dfrac{\partial \varphi_1}{\partial x_1}(\m{a}) & \ldots & \dfrac{\partial \varphi_1}{\partial x_m}(\m{a}) & \dfrac{\partial \varphi_1}{\partial x_{m+1}}(\m{a}) & \ldots & \dfrac{\partial \varphi_1}{\partial x_{m+n}}(\m{a}) \\
\vdots & \ddots & \vdots & \vdots & \ddots & \vdots\\
\dfrac{\partial \varphi_m}{\partial x_1}(\m{a}) & \ldots & \dfrac{\partial \varphi_m}{\partial x_m}(\m{a}) & \dfrac{\partial \varphi_n}{\partial x_{m+1}}(\m{a}) & \ldots & \dfrac{\partial \varphi_m}{\partial x_{m+n}}(\m{a}) \\
0 & \ldots & 0 & 1 & \ldots &0 \\
\vdots & \ddots & \vdots & \vdots & \ddots & \vdots\\
0 & \ldots & 0 & 0 & \ldots & 1
\end{pmatrix} \\
&= \lambda_1 (\mathrm{d}\varphi_1)_{\m{a}} + \ldots + \lambda_m (\mathrm{d}\varphi_m)_{\m{a}},
\end{align*} ( d f ) a = ( d f u ) Φ ( a ) ⋅ ( d Φ ) a = ( λ 1 … λ m 0 … 0 ) ⎝ ⎛ ∂ x 1 ∂ φ 1 ( a ) ⋮ ∂ x 1 ∂ φ m ( a ) 0 ⋮ 0 … ⋱ … … ⋱ … ∂ x m ∂ φ 1 ( a ) ⋮ ∂ x m ∂ φ m ( a ) 0 ⋮ 0 ∂ x m + 1 ∂ φ 1 ( a ) ⋮ ∂ x m + 1 ∂ φ n ( a ) 1 ⋮ 0 … ⋱ … … ⋱ … ∂ x m + n ∂ φ 1 ( a ) ⋮ ∂ x m + n ∂ φ m ( a ) 0 ⋮ 1 ⎠ ⎞ = λ 1 ( d φ 1 ) a + … + λ m ( d φ m ) a , что и требовалось доказать.