Подпространства метрического пространства - The Hitchhiker's Guide to the Calculus Galaxy

Пусть $F \subseteq E$ — непустое подмножество метрического пространства $E$ с расстоянием $d$ , тогда $F \times F \subseteq E \times E$ — непустое подмножество, тогда мы имеем следующую коммутативную диаграмму

т. е., сужая метрику $d$ на $F$ , мы получаем метрическое пространство $(F,d|_{F \times F})$ , которое мы будем для простоты обозначать $(F, d_F)$ .

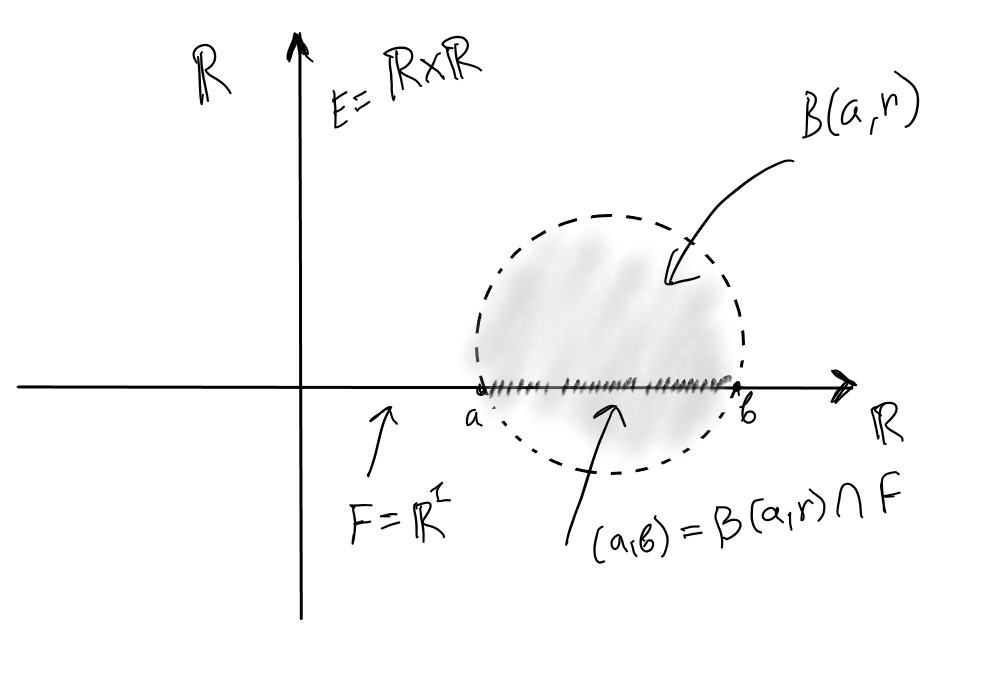
Пусть E = \mathbb{R} \times \mathbb{R} — обыкновенная плоскость с обыкновенной евклидовой метрикой d(\m{x},\m{y}) = \sqrt{(x_1 - y_1)^2+ (x_2 - y_2)^2}, и пусть F = \mathbb{R}, которую мы можем понимать как множество вида \{(x,0), x\in \mathbb{R}\}. На рисунке F отождествлена с осью Ox. Тогда, сужая метрику d на F, мы получаем, что d(x,y) = \sqrt{(x-y)^2} = |x-y|. Более того, ясно, что любой интервал (a,b) можно получить, пересекая открытый круг с F. — Пусть $E = \mathbb{R} \times \mathbb{R}$ — обыкновенная плоскость с обыкновенной евклидовой метрикой $d(\m{x},\m{y}) = \sqrt{(x_1 - y_1)^2+ (x_2 - y_2)^2}$ , и пусть $F = \mathbb{R}$ , которую мы можем понимать как множество вида $\{(x,0), x\in \mathbb{R}\}$ . На рисунке $F$ отождествлена с осью $Ox$ . Тогда, сужая метрику $d$ на $F$ , мы получаем, что $d(x,y) = \sqrt{(x-y)^2} = |x-y|$ . Более того, ясно, что любой интервал $(a,b)$ можно получить, пересекая открытый круг с $F.$

Proof

Прежде всего, поймём, что есть открытый шар в $F$ . Пусть $a \in F$ , и рассмотрим открытый шар $B(a,r) \subseteq E$ , тогда получаем

\begin{align*} F \cap B(a,r) &:=& \{x \in E \cap F\, :\, d(x,a)<r\} \\ &=&\{x\in F\, :\, d(x,a)<r\} \\ &=& \{x \in F\, :\, d_F(x,a)<r\}, \end{align*}

(1)

т. е. $F \cap B(a,r)$ — это открытый шар в $F$ с центром в точке $a$ радиуса $r.$

Warning

Обратим внимание, что если $F = \mathbb{R}_{\ge 0} \subseteq \mathbb{R} = E$ , $d(x,y) = |x-y|$ , то, например, $[0,1)$ — открытый шар в $F = \mathbb{R}_{\ge 0}$ , так как $[0,1) = (-1,1) \cap \mathbb{R}_{\ge 0}$ . Hо! В $\mathbb{R}$ , $[0,1)$ и не открыт и не замкнут!

(1) Пусть $\mathscr{U}$ — открытое множество в $E$ , и пусть $x \in \mathscr{U} \cap F$ . Так как $\mathscr{U}$ — открытое в $E$ , то найдётся шар $B(x,r) \subseteq E$ такой, что $B(x,r) \subseteq \mathscr{U}$ . Тогда $F \cap B(x,r) \subseteq F \cup \mathscr{U}$ . Но мы уже поняли, что $B(x,r) \cap F$ — открытый шар в $F$ , но тогда включение $F \cap B(x,r) \subseteq F \cup \mathscr{U}$ и означает, что $\mathscr{U} \cap F$ открыто в $F$ , ибо $x$ — произвольная точка в $\mathscr{U} \cap F.$ (2) Пусть $S$ открыто в $F$ , это значит, что для любой точки $x \in S$ можно найти открытый шар $B(x, r(x)) \subseteq E$ такой, что $F \cap B(x,r(x)) \subseteq S$ (т.к., $F \cap B(x,r(x))$ — это открытый шар в $F$ ). Тогда

S = \bigcup_{x \in S} F \cap B(x, r(x)) = F \cap \mathscr{U},

(2)

где $\mathscr{U} = \cup_{x\in S} B(x, r(x)) \subseteq E$ , тогда по Леммам Lemma 1, [](#union_and_cap_of_open} $\mathscr{U}$ открыто в $E$ .

Метрические пространства

Замкнутые множества, точки замыкания (=точки прикосновения), замыкание множества.

Метрические пространства

Пределы