Метрические пространства

Определим метрическое пространство. Пусть $E$ — некоторое множество. Расстояние в $E$ есть отображение $d:E\times E \to \mathbb{R}_{\ge 0}$ , обладающее следующими свойствами:

$d(x,y) = 0$ , если и только если $x = y$ .
$d(x,y)=d(y,x)$ , для любых $x,y \in E$ .
$d(x,z) \le d(x,y) + d(y,z)$ , для любых трёх $x,y,z\in E$ (неравенство треугольника).

1Примеры расстояний¶

Функция $d(x,y):=|x-y|$ есть расстояние в множестве $\mathbb{R}$ действительных чисел.
В $\mathbb{R}^2$ обычное евклидово расстояние определяется формулой
$d(\m{x}, \m{y}):= \sqrt{(x_1 -y_1)^2 + (x_2 - y_2)^2},$
где $\m{x} = (x_1,x_2)$ , $\m{y} = (y_1,y_2).$
На плоскости $\mathbb{R}^2$ можно также ввести расстояние следующим образом:
$d(\m{x},\m{y}):= |x_1-y_1| + |x_2-y_2|.$
Ещё один пример расстояния на плоскости:
$d(\m{x},\m{y}):=\max\{|x_1 - y_1|, |x_2 - y_2|\}.$

2Изометрия¶

Пусть $E,E'$ — два метрических пространства, $d,d'$ — расстояния в $E$ и $E'$ . Биективное отображение $f:E \to E'$ называется изометрией, если

d'(f(x), f(y)) = d(x,y)

для любой пары элементов пространства $E$ обратное отображение $f^{-1}$ является изометрией пространства $E'$ на $E$ . Два метрических пространства называются $E,E'$ изометричны, если существует изометрия $E$ на $E'$ .

Пусть $E$ — метрическое пространство, $d$ — расстояние в $E$ и $f$ — биективное отображение $E$ на какое-то множество $E'$ ^[1] Мы можем тогда определить в $E'$ расстояние $d'$ как выше, т. е.

d'(f(x), f(y)) = d(x,y),

и в таком случае $f$ будет изометрией пространства $E$ в $E'$ . Говорят, что расстояние $d'$ было перенесено с $E$ на $E'$ отображением $f.$

3Расширенная действительная прямая $\overline{\mathbb{R}}$ и как измерять расстояние до бесконечности¶

Функция $f$ , определённая на $\mathbb{R}$ условием

f(x) = \frac{x}{1+ |x|},

является биективным отображением $f:\mathbb{R} \to (-1,1)$ . Обратное отображение определяется формулой

f^{-1}(x) = \frac{x}{1- |x|}

при $|x|<1.$

Обозначим через $\overline{\mathbb{R}}$ множество, являющееся объединением $\mathbb{R}$ и двух новых элементов, обозначаемых символами $+\infty$ и $- \infty$ (=бесконечные точки).

Тем самым, мы имеем вложение (инъекцию) $\mathbb{R} \hookrightarrow \overline{\mathbb{R}}$ . Продолжим $f$ до биективного отображения $\overline{f}: \overline{\mathbb{R}} \to [0,1]$ , полагая

\overline{f}(x) = \begin{cases} f(x), & x \in \mathbb{R},\\ 1, & x = \infty,\\ -1, & x = - \infty. \end{cases}

Тогда

\overline{f^{-1}}(x) = \begin{cases} f^{-1}(x), & x \in (0,1),\\ \infty, & x = 1,\\ -\infty, & x = - 1. \end{cases}

Теперь мы можем ввести расстояние на $\overline{\mathbb{R}}$ , $\overline{d}(x,y):=|\overline{f}(x) - \overline{f}(y)|$ , $x,y \in \overline{\mathbb{R}}.$ Более подробно,

\begin{align*} \overline{d}(x,y) &=& \left| \frac{x}{1+|x|} - \frac{y}{1+|y|} \right|, \qquad x,y\in \mathbb{R}\\ d(x, + \infty) &=& \frac{1}{1+|x|}, \qquad x \ge 0\\ d(-\infty,x) &=& \frac{1}{1+|x|}, \qquad x \le 0. \end{align*}

На $\overline{R}$ введём отношение порядка, по определению считая неравенство $x \le y$ эквивалентным неравенству $f(x) \le f(y)$ . Легко проверить, что когда $x,y \in \mathbb{R}$ , это отношение порядка есть обычное отношение порядка на $\mathbb{R}$ и что, кроме того, для любого $x\in \mathbb{R}$ мы имеем $- \infty < x < \infty.$

Действительные числа называются также конечными элементами $\overline{\mathbb{R}}.$

4Шары и сферы¶

Элементы метрического пространства будем также называть точками.

5Открытые множества и окрестности¶

Proof

Пусть $B(a,r)$ — открытый шар, по аксиоме выбора мы можем взять точку $x \in B(a,r)$ , $x \ne a$ . Тогда по определению $d(x,a) < r$ . Рассмотрим теперь открытый шар $B(x,\delta)$ , где $0 < \delta < r- d(a,x).$ Покажем, что $B(x,\delta ) \subseteq B(a, r)$ , это и докажет лемму.

По аксиоме выбора мы можем взять такое $y \in B(a,\delta)$ , что $d(x,y)<\delta < r - d(a,x)$ , тогда по неравенству треугольника

d(a,y) \le d(a,x) + d(x,y) < d(a,x) + r - d(a,x) = r,

т. е. $y\in B(a,r)$ , что и доказывает $B(x,\delta) \subseteq B(a,r)$ . Так как точка $x$ была выбрана произвольной в шаре $B(a,r)$ , это показывает, что для любой точки в шаре мы нашли такой открытый шар, который целиком лежит в $B(a,r)$ , т. е. он открыт.

Proof

(1) Пусть $\mathscr{U} = \cup_{\alpha \in A}\mathscr{U}_\alpha$ и пусть $x \in \mathscr{U}$ , тогда для какого-то $\alpha \in A$ , $x \in \mathscr{U}_a$ . Так как $\mathscr{U}_\alpha$ — открыто, то найдётся такой $r >0$ , что $B(x, r ) \subseteq \mathscr{U}_\alpha \subseteq \cup_{\alpha \in A}\mathscr{U}_\alpha$ , что и доказывает открытость $\mathscr{U}.$

(2) Достаточно доказать, что множество двух открытых множеств $\mathscr{U}_1, \mathscr{U}_2$ открыто, а затем провести индукцию. Если $x \in \mathscr{U}_1 \cap \mathscr{U}_2$ , то найдутся такие $r_1, r_2 >0$ , что $B(x, r_1) \subseteq \mathscr{U}_1$ , $B(x, r_2) \subseteq \mathscr{U}_2$ . Очевидно, что $B(x, r) \subseteq \mathscr{U}_1 \cap \mathscr{U}_2$ , где $r:= \min(r_1, r_2)$ , что и доказывает открытость пересечения.

6Непрерывные отображения¶

Definition 4

Пусть $E$ , $E'$ — два метрических пространства, $d$ и $d'$ — расстояния в них. Отображение $f:E \to E'$ называется непрерывным в точке $x_0 \in E$ , если для каждой окрестности $\mathscr{U}'$ точки $f(x_0) \in E'$ существует такая окрестность $\mathscr{U}(x_0)$ в $E$ , что $f(\mathscr{U}(x_0)) \subseteq \mathscr{U}'(f(x_0))$ . Отображение $f$ называется непрерывным в $E$ (или просто непрерывным), если оно непрерывно в каждой точке пространства $E.$

Это же определение можно переформулировать и таким образом:

Можно ещё вот так сказать:

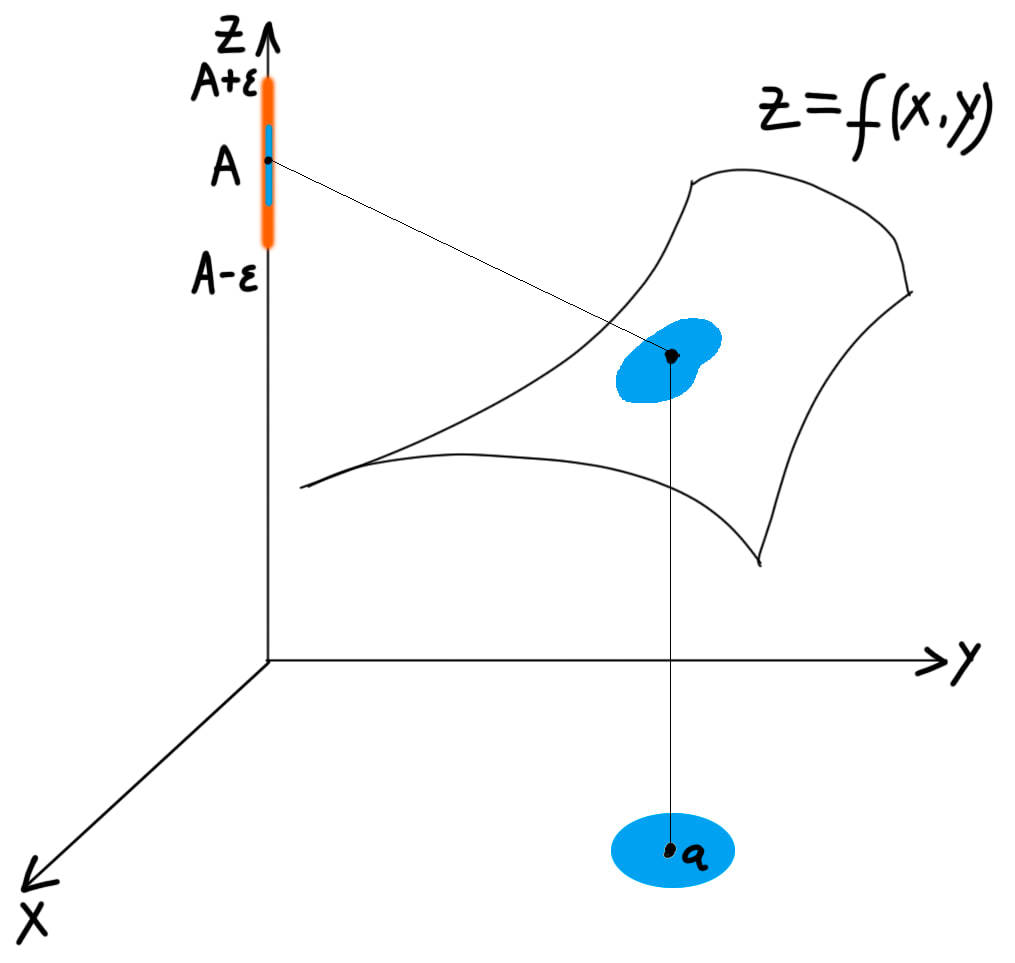
График отображения f: \mathbb{R}^2 \to \mathbb{R} есть некоторая поверхность в \mathbb{R}^3. Нужно понимать, что мы горизонтальную плоскость отображаем в вертикальную прямую. Здесь показано, почему в точке \m{a}\in \mathbb{R}^2 это отображение непрерывно, f(\m{a}) = A. Какой бы оранжевый шар \textcolor{orange}{B(A, \varepsilon)} \subseteq \mathbb{R} мы не взяли, можно найти синий шар \textcolor{blue}{B(\m{a},r)} \in \mathbb{R}^2 такой, что его образ f( \textcolor{blue}{B(\m{a}, r)} ) в вертикальной прямой (синяя полоска в оранжевом отрезке) будет целиком содержаться в этом оранжевом шаре. — График отображения $f: \mathbb{R}^2 \to \mathbb{R}$ есть некоторая поверхность в $\mathbb{R}^3$ . Нужно понимать, что мы горизонтальную плоскость отображаем в вертикальную прямую. Здесь показано, почему в точке $\m{a}\in \mathbb{R}^2$ это отображение непрерывно, $f(\m{a}) = A$ . Какой бы оранжевый шар $\textcolor{orange}{B(A, \varepsilon)} \subseteq \mathbb{R}$ мы не взяли, можно найти синий шар $\textcolor{blue}{B(\m{a},r)} \in \mathbb{R}^2$ такой, что его образ $f( \textcolor{blue}{B(\m{a}, r)} )$ в вертикальной прямой (синяя полоска в оранжевом отрезке) будет целиком содержаться в этом оранжевом шаре.

Example 2

Пусть $E = E' = \mathbb{R}$ с одинаковой метрикой $d(x,y) = |x-y|$ , покажем, что отображение $\overline{f}:E \to E'$ ;

\overline{f}(x) = \begin{cases} x^2 \sin \frac{1}{x}, & x \ne 0, \\ 0, & x =0 \end{cases}

непрерывно в точке 0.

Это значит, что для любого $\varepsilon >0$ мы должны найти такую $\delta >0$ , что из неравенства $|x|<\delta$ будет следовать $|\overline{f}(x) - \overline{f}(0)| <\varepsilon.$ Чтобы найти такую δ, мы заметим, что

\overline{f}(x) -\overline{f}(0)| = |x^2 \sin \frac{1}{x} - 0 | = |x^2 \sin \frac{1}{x}| \le |x^2| = x^2,

поэтому если $x^2 <\varepsilon$ , т. е. $-\sqrt{ \varepsilon} <x < \sqrt{\varepsilon}$ , то и $|\overline{f}(x) - \overline{f}(0)| <\varepsilon$ . Значит, для любого $0 < \delta < \sqrt{\varepsilon}$ из неравенства $|x|<\delta$ вытекает неравенство $|\overline{f}(x) - \overline{f}(0)|$ , что и доказывает непрерывность в точке 0.

Proof

(1) Пусть $f:E \to E'$ непрерывно. Возьмём открытое $\mathscr{U}' \subseteq E'$ и покажем, что $\mathscr{U}:=f^{-1}(\mathscr{U'})$ открыто в $E$ . Пусть $x \in \mathscr{U}$ , тогда $f(x) = x' \in \mathscr{U}'$ , так как $\mathscr{U}'$ — открыто в $E'$ , то найдётся шар $B'(x',r') \subseteq \mathscr{U}'$ . Так как шар $B'(x',r')$ есть открытая окрестность точки $x'$ и по предположению $f$ непрерывна и в точке $x \in E$ , значит, найдётся такой шар $B(x,r) \subseteq E$ такой, что $f(B(x,r)) \subseteq B'(x',r')$ .

Таким образом, мы имеем $f(B(x,r)) \subseteq B'(x',r') \subseteq \mathscr{U}' .$ С другой стороны, если $A'\subseteq B' \subseteq E'$ , то ясно, что $f^{-1}(A') \subseteq f^{-1}(B')$ . Действительно, по определению прообраза

f^{-1}(A'):= \{x \in X\, |\, f(x) \in A' \subseteq B'\} \Longrightarrow f^{-1}(A') \subseteq f^{-1}(B').

Итак, мы получили, что $f(B(x,r)) \subseteq B'(x',r') \subseteq \mathscr{U}'$ , тогда

f(B(x,r)) \subseteq \mathscr{U}' \Longleftrightarrow f^{-1}(f(B(x,r))) \subseteq f^{-1}(\mathscr{U}') \Longleftrightarrow B(x,r) \subseteq \mathscr{U},

т. е. для любого $x \in \mathscr{U}$ мы нашли шар $B(x,r)$ , который целиком находится в $\mathscr{U}$ , а это и означает, что $\mathscr{U}$ открыто.

(2) Пусть прообраз любого открытого есть открытое множество в $E.$ Пусть $\mathscr{U}'$ — открытое в $E'$ . Аксиома выбора позволяет нам выбрать точку $x' \in \mathscr{U}'$ . Тогда для произвольно выбранной точки $x'$ существует такой открытый шар $B'(x',r')$ , что $B'(x',r') \subseteq \mathscr{U}'.$

Пусть $f(x) = x'$ , т. е. $x \in f^{-1}(B'(x',r'))$ . По предположению $f^{-1}(B'(x',r'))$ открыто в $E$ . Это значит, что для любой выбранной точки $y \in f^{-1}(B'(x',r'))$ можно найти такой открытый шар $B(y,r)$ , что $B(y,r) \subseteq f^{-1}(B'(x',r'))$ . В частности, $B(x,r) \subseteq f^{-1}(B'(x',r'))$

Вспоминая, что если $A \subseteq B$ , то и $f(A) \subseteq f(B)$ . Тогда получаем

B(x,r) \subseteq f^{-1}(B'(x',r')) \Longrightarrow f(B(x,r)) \subseteq f(f^{-1}(B'(x',r'))) \subseteq B'(x',r'),

т. е. для любого открытого шара $B'(x',r')$ , где $x' = f(x)$ , мы нашли такой открытый шар $B(x,r)$ , что $f(B(x,r)) \subseteq B'(x',r')$ , но это и означает непрерывность.

Proof

Это сразу следует из предыдущей теоремы и леммы Lemma 3.1.4.

Proof

Второе утверждение, очевидно, следует из первого. Пусть $\mathscr{U}''$ — окрестность точки $h(x_0) = g(f(x_0))$ . Тогда из предположения о непрерывности и Теоремы Theorem 4.1.1 следует, что $\mathscr{U}':=g^{-1}(\mathscr{U}'')$ — открытое множество в $E'$ , содержащее точку $f(x_0)$ . Далее, так как $f$ непрерывно, то по теореме Lemma 1.5.1, прообраз $\mathscr{U}:=f^{-1}(\mathscr{U}')$ — открытое множество, содержащее точку $x_0$ . Таким образом, $h^{-1}(\mathscr{U}'') = \mathscr{U}$ открытое, тогда по теореме Theorem 4.1.1, $h$ непрерывно в точке $x_0$ , что и завершает доказательство.

Proof

На самом деле, $f$ непрерывно в $x_0$ по условию, а $\mathrm{in}_A$ непрерывно в любой точке $a \in A$ , тогда из предыдущей теоремы и следует утверждение.

Remark 2

Пусть $E = \overline{\mathbb{R}}$ — расширенная прямая, рассмотрим выражение $\lim_{x \to +\infty, x \in \mathbb{{R}}}f(x) = a'$ , где $f:\mathbb{R} \to E'$ — некоторое отображение. Мы знаем, что $B(+\infty, \delta) = (\frac{1-\delta}{\delta}, \infty]$ . Тогда непрерывность в точке $+\infty$ означает, что для любого $r >0$ найдётся такая $\delta>0$ , что $f((\frac{1-\delta}{\delta}, \infty]) \subseteq B(a',r)$ . Другими словами, для любого шара $B(a',r)$ найдётся такое число $\alpha \in \mathbb{R}$ , что $f(\beta) \in B(a',r)$ для всех $\beta > \alpha.$

Footnotes¶

В $E'$ до этого расстояние могло быть и не определено.
↩

Метрические пространства

Пространства в ℝⁿ

Метрические пространства

Замкнутые множества, точки замыкания (=точки прикосновения), замыкание множества.

1Примеры расстояний¶

2Изометрия¶

3Расширенная действительная прямая R‾\overline{\mathbb{R}}R и как измерять расстояние до бесконечности¶

4Шары и сферы¶

5Открытые множества и окрестности¶

6Непрерывные отображения¶

3Расширенная действительная прямая $\overline{\mathbb{R}}$ и как измерять расстояние до бесконечности¶