Полином Тейлора от нескольких переменных - The Hitchhiker's Guide to the Calculus Galaxy

Прежде всего рассмотрим следующую задачу. Пусть нам дана функция $\psi:\mathbb{R}^n \to \mathbb{R}$ . Допустим что она дифференцируема в окрестности $\mathscr{U}$ точки $\m{a} = (a_1,\ldots, a_n)$ , и пусть при $0\le t \le 1$ , точка $\m{a}+t\m{h} = (a_1 + th_1, \ldots, a_n+th_n)$ также принадлежит этой же окрестности. Тогда, при фиксированных $\m{a}, \m{h}$ мы уже получаем функцию $\psi(\m{a}+t\m{h})$ от одной переменной. Как найти её производную?

Lemma 1

Пусть $f:\mathbb{R}^n \to \mathbb{R}$ дифференцируема в окрестности точки $\mathscr{U}$ точки $\m{a}$ , и пусть при $0\le t \le 1$ , точка $\m{a}+t\m{h}\in \mathscr{U}$ . Тогда, при фиксированных $\m{a}, \m{h}$ , функция $\psi_{\m{a},\m{h}}(t):= f(\m{a}+t\m{h}):\mathbb{R} \to \mathbb{R}$ дифференцируема при $0 \le t \le 1$ и

\psi_{\m{a},\m{h}}'(t) = \left.\frac{\partial f}{ \partial x_1}\right|_{\m{a} + t \m{h}} \cdot h_1 + \cdots + \left.\frac{\partial f}{ \partial x_n}\right|_{\m{a} + t \m{h}} \cdot h_n

Proof

Прежде всего мы видим, что наша функция $\psi_{\m{a},\m{h}}(t)$ есть композиция двух стрелок

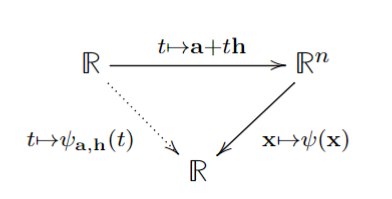
Далее, для функции от одной переменной, значение её производной это есть значение дифференциала вычисленного в этой же точке. Тогда по теореме о композиции Theorem 1,

\psi'_{\m{a},\m{h}}(t) = (\mathrm{d}\psi)_t = (\mathrm{d}f)_{\m{a}+t\m{h}} \cdot (\mathrm{d}\gamma)_t,

где

\gamma(t): = \m{a}+t\m{h} = \begin{pmatrix} a_1 + th_1 \\ \vdots \\ a_n + t h_n \end{pmatrix}

Тогда её матрица Якоби (=дифференциал) имеет вид

\mathrm{d}\gamma = \begin{pmatrix} \dot\gamma_1(t) \\ \vdots \\ \dot \gamma_n(t) \end{pmatrix} = \begin{pmatrix} h_1 \\ \vdots\\ h_n \end{pmatrix} = \m{h},

здесь $\gamma_1(t) = a_1 + th_1,\ldots, \gamma_n(t) = a_n+th_n.$ Тогда, получаем

\begin{align*} \psi'_{\m{a},\m{h}}(t) & =& (\mathrm{d}\psi)_t = (\mathrm{d}f)_{\m{a}+t\m{h}} \cdot (\mathrm{d}\gamma)_t \\ &=& (\mathrm{d}f)_{\m{a}+t\m{h}} \m{h} \\ &=& \left.\frac{\partial f}{ \partial x_1}\right|_{\m{a} + t \m{h}} \cdot h_1 + \cdots + \left.\frac{\partial f}{ \partial x_n}\right|_{\m{a} + t \m{h}} \cdot h_n, \end{align*}

что и требовалось доказать.

Proof

Пусть $\varphi_{\m{a},\m{h}}(t): = f(\m{a}+t \m{h})$ , $t \in [0,1]$ , тогда согласно Следствию Corollary 1, она $m+1$ раз дифференцируема и более того

\varphi^{k}(t) = (\mathrm{d}^k_{\m{a}+t\m{h}}f)(\m{h}).

Тогда её полином Тейлора с остаточным мономом в форме Лагранжа (Следствие Corollary 2 имеет вид

\varphi(t) = \varphi(0) + \frac{\varphi'(0)}{1!}t + \frac{\varphi''(0)}{2!}t^2 + \cdots + \frac{\varphi^{(m)}(0)}{m!}t^m + \frac{\varphi^{(m+1)}(\theta)}{(m+1)!}t^{m+1}

где $0 < \theta < t.$

Тогда, используя равенство

\varphi_{\m{a},\m{h}}^{k}(t) = (\mathrm{d}^k_{\m{a}+t\m{h}}f)(\m{h}), \qquad 1 \le k \le m+1.

получаем

\begin{align*} \varphi(0) &=& f(\m{a}), \\ \varphi^{(k)}(0) &=& (\mathrm{d}^k_{\m{a}}f)(\m{h}), \qquad 1 \le k \le m,\\ \varphi^{(m+1)}(\theta) &=&(\mathrm{d}^{m+1}_{\m{a}+\theta \m{h}}f)(\m{h}). \end{align*}

Тогда мы можем записать

\varphi(t) = f(\m{a}) + \sum_{k=1}^m \frac{(\mathrm{d}^k_{\m{a}}f)(\m{h})}{k!}t^k + \frac{( \mathrm{d}^{m+1}_{\m{a}+\theta \m{h}}f)(\m{h}) }{(m+1)!}t^{m+1},

так как $\varphi(1) = f(\m{a}+\m{h})$ , то подставляя $t=1$ в последней сумме мы получаем требуемое.

Анализ в ℝⁿ

Высшие дифференциалы

Анализ в ℝⁿ

Компактные пространства